Is There a Future for Nuclear Power in the United States?

Whither nuclear power? That question has become more important as energy policies evolve to emphasize emissions-free “green” energy and an increased electrification of the U.S. economy. Some environmentalists consider nuclear power to be crucial to reducing carbon emissions; others continue to vehemently oppose nuclear power and believe that our energy must come solely from renewable sources. Asked whether they favor or oppose nuclear power, the public is split.*
Meanwhile, the nuclear power industry itself is in a parlous state for a variety of reasons. These include: (i) decades of construction cost overruns and plant delays because of poor designs, lack of manufacturing expertise, and changing regulations; (ii) political squabbling over spent nuclear fuel disposal; (iii) energy policies, including renewable energy subsidies and mandates, that have distorted electric power markets and made it harder for nuclear plants to compete; and (iv) lower natural gas prices and more efficient gas-fired generators. In the past few years, threatened plant closures have led state policymakers to award subsidies to a number of existing plants, and more such subsidies are likely forthcoming.
Nevertheless, nuclear power provides valuable benefits. It is highly reliable and emissions-free. It provides generation diversity, which can reduce the adverse impacts of fuel price shocks. It does not require backup and storage, unlike wind and solar power generation. New designs for nuclear plants promise lower costs and improved safety. This paper thus concludes that saving nuclear power is crucial to this country’s energy future, especially if that future is based on increased electrification.
Several policies are necessary to preserve this power source. They include:
- Eliminating subsidies for renewable energy at the state and federal level, including federal production tax credits, state renewable portfolio standards, and feed-in tariffs for renewable resources that are increasingly distorting wholesale electric markets.
- Linking subsidies for existing nuclear plants to wholesale market prices of electricity and combining them with performance incentives that require improved operating efficiency over time. However, before subsidies are granted to prevent a nuclear plant’s closure, a comprehensive cost-benefit analysis should be performed to ensure that the grant is not a futile exercise or is so costly that building replacement generating capacity is a lower-cost alternative.
- Providing government loan guarantees for the construction of new nuclear plants. But these guarantees must require investors to bear a portion of the financial risk and require developers to prove that their reactors are safer and more reliable than existing ones.
- Developing public-private partnerships that will leverage existing nuclear-focused Department of Energy (DOE) facilities like the Idaho National Laboratory and the Oak Ridge National Laboratory. Those labs can be used to test and evaluate new nuclear technologies. Test reactor sites can also be used to validate more efficient manufacturing techniques.
- Solving the current political logjam over a permanent spent-fuel repository by identifying communities near geologically suitable sites that wish to host such a depository with the promise of local jobs and improved economic growth.
*R. J. Reinhart, “40 Years After Three Mile Island, Americans Split on Nuclear Power,” Gallup, Mar. 27, 2019. Gallup reported that 49% of the public favor nuclear power, and 49% oppose it. On safety, 47% say that nuclear power plants are safe, and 49% say that they are not safe.
Introduction
The domestic nuclear power industry is in the midst of a decades-long decline. The causes are many. Plant construction costs that spiraled out of control because of “one-off” designs and changing regulatory requirements, decreases in electricity demand growth that eliminated the need for planned units, and irrational fears of nuclear accidents have all taken their toll on the industry. More recently, environmental and political opposition has caused some nuclear plant owners to agree to retire plants prematurely—including Exelon’s Oyster Creek plant in New Jersey, Indian Point in New York, and Diablo Canyon in California—rather than face costly and protracted litigation. Lastly, the decline in natural gas prices and changes in wholesale electric market designs—including subsidies for wind and solar generation—have also adversely affected nuclear plant profitability, especially for smaller, single-reactor plants.
These factors have caused a number of U.S. nuclear plants to be shuttered before the end of their useful lives. Currently, 11 of the 60 operating plants, with a total capacity of 17,000 megawatts (MW) and producing about 125 terawatt-hours (TWh) of electricity annually (enough to power more than 12 million homes),[1] are slated for closure by 2025. By comparison, in 2018, the 30,000 MW of utility-scale solar photovoltaics (PV) and 94,000 MW of wind power in the country produced 63 TWh and 275 TWh, respectively.[2] The total generating capacity of the nation’s nuclear plants is a little over 99,000 MW, about the same as wind power. Yet in 2018, nuclear generation totaled over 800 TWh, more than double the amount of wind and solar PV generation combined. (One key reason that nuclear produces so much more electricity than solar or wind for a given amount of capacity is that solar and wind are inherently intermittent energy sources while nuclear plants are designed to run all the time.)
Nuclear plant subsidies have been justified in order to recognize “unpriced” benefits, such as “zero-emissions credits” (ZECs) in Illinois and New York.[3] Some states have also been keen to ensure that nuclear plants continue to operate because of the jobs and economic benefits they provide to local communities, many of which would suffer adverse economic impacts from closures. Whether the benefits of such subsidies exceed their costs, which are paid by electric ratepayers and have their own adverse impacts, is an empirical question. (Ironically, while New York now subsidizes three upstate nuclear plants, Governor Andrew Cuomo led the efforts to shutter the Indian Point facility, about 40 miles north of Manhattan on the Hudson River. One of its two generating units is scheduled to be shut next year; the other is set to be closed in 2022.) Subsidies for nuclear plants were recently approved in New Jersey[4] and Connecticut.[5] Legislation to subsidize nuclear plants in Ohio and Pennsylvania has also been introduced.
As for constructing new plants, despite regulatory reforms and promises of standardized designs, construction efforts have faltered because of crippling cost overruns, continuing a multidecade pattern. Overruns led to the abandonment of the uncompleted Santee Cooper plant in South Carolina in 2017. The estimated cost of two new reactors at the Southern Company’s Vogtle plant in Georgia has roughly doubled, to over $27 billion, while the scheduled online completion date for the first of the new reactors has slipped from 2017 to 2022, at the earliest.[6]
In addition to the problems listed above, the nuclear sector has yet to resolve the issue of waste disposal.[7] Furthermore, nuclear energy opponents have exploited the public’s fears of this power source—which arose from the accidents at Three Mile Island (TMI) in Pennsylvania in 1979, Chernobyl in Ukraine in 1986, and the tidal wave that engulfed Japan’s Fukushima-Daiichi plant in 2011.
 Yet the nuclear plants that operate today do so more efficiently and economically than ever; they generate more power and at lower costs than in years past.[8] In part, this is the result of changes in wholesale electricity markets that spurred competition and provided economic incentives to reduce costs and increase profitability, in contrast to traditional cost-of-service regulatory regimes that provide virtually no incentives to do so. For the last 30 years, nuclear power has provided about 20% of all U.S. electricity generation. (In 2018, the share was just over 21%.) By comparison, despite decades of subsidies for renewable generation and various state mandates to develop increasing quantities of such generation, non-hydroelectric renewables provided less than 9% of total U.S. electricity generation last year (Figure 1).
Yet the nuclear plants that operate today do so more efficiently and economically than ever; they generate more power and at lower costs than in years past.[8] In part, this is the result of changes in wholesale electricity markets that spurred competition and provided economic incentives to reduce costs and increase profitability, in contrast to traditional cost-of-service regulatory regimes that provide virtually no incentives to do so. For the last 30 years, nuclear power has provided about 20% of all U.S. electricity generation. (In 2018, the share was just over 21%.) By comparison, despite decades of subsidies for renewable generation and various state mandates to develop increasing quantities of such generation, non-hydroelectric renewables provided less than 9% of total U.S. electricity generation last year (Figure 1).
Nuclear power offers some obvious benefits over renewable resources. Unlike wind and solar power, nuclear is always on and needs no backup. Nuclear plants also do not require vast swaths of land. Moreover, nuclear provides “resilience” to the bulk power system, acting as a stabilizing force that can lessen the impact of severe weather events and other disruptions. (The bulk power system is the network of generators and transmission lines that delivers electricity to local utilities, which distribute that power to customers.) Some environmentalists, concerned about carbon emissions and climate change, believe that nuclear power is the only realistic way of reducing those emissions enough to halt the damage.
For those and other reasons, nuclear power has not been abandoned. The federal government continues to fund research into new plant designs. In September 2018, the Nuclear Energy Innovation Capabilities Act (NEICA) was signed into law.[9] NEICA reduces regulatory costs for nuclear plant developers and provides funding for facilities to test new types of reactors. The Nuclear Regulatory Commission (NRC) is proposing new rules designed to streamline siting and licensing requirements as well as address the costs of ensuring that the plants are secure from outside threats. Small modular reactors (SMRs) promise true modular construction, passive safety systems that do not require active intervention by plant operators to shut down a reactor, and lower costs. New research is even examining the potential for micro-scale nuclear plants, with output ranging from 1 to 10 MW, to serve defense installations and remote facilities, such as mining operations in the Arctic.[10]
Unfortunately, the costs of constructing new plants in the U.S. have, if anything, increased, owing in part to a loss of know-how. Because the building of nuclear plants here has been largely dormant for decades, the expertise of construction companies active in the field in the 1970s and 1980s is mostly gone, requiring new builders to reinvent the wheel. Furthermore, although most experts agree that disposal of spent nuclear fuel is not a technological issue, political opposition has stalled development of a permanent repository for such fuel at Yucca Mountain, in Nevada. If the nuclear industry is to survive, the political and environmental opposition to siting a permanent repository must be addressed.
The more difficult policy questions are: (i) whether nuclear power should play a future role in supplying the nation’s electricity; and, if so, (ii) what market and policy changes are needed to reduce construction costs and restore the industry’s economic viability? These questions take on far greater importance in light of some states establishing zero-emissions mandates that will require electrifying their entire economies,[11] as well as the recent proposal for a “Green New Deal,” which calls for “net-zero” carbon emissions within 10 years and ultimate abandonment of all fossil-fuel use, among other objectives.[12]
The short answer is that the goal of supplying the nation with sufficient amounts of zero-emission and reliable electricity cannot be met without nuclear power. The inherent intermittency of wind and solar generation—along with the huge land areas that would be required,[13] both for the generating capacity itself and the battery storage needed to “firm up” these resources—makes that goal unrealistic without nuclear, even if wind, solar, and battery technologies continue to improve.[14] The costs of providing backup battery storage and acquiring vast tracts to site utility-scale wind and solar generation are simply prohibitive. Thus, barring development and commercialization of entirely new emissions-free generation technologies, the nuclear industry must be revived.
But doing so will require overcoming two significant hurdles that have plagued the industry since its inception. First, the cost of new plants must be reduced. The most promising way to do so appears to be adoption of modular construction techniques, in contrast to the one-off designs of most existing U.S. plants. Second, the political roadblocks associated with siting a permanent spent-fuel depository must be removed. The former cannot be accomplished without government subsidies and loan guarantees. The latter likely cannot be accomplished unless the approach to siting a permanent depository is changed.
Reviving the nuclear industry also raises the question of what to do about existing plants, some of which cannot compete in wholesale energy markets. In part, this is due to subsidies provided to wind and solar generation. And, in some cases, it stems from the complexities of how wholesale power markets are designed.[15] But it is primarily the result of low-cost natural gas supplies and improvements in gas-fired generation technology. Those improvements have benefited both the environment—because natural gas is cleaner than the coal-fired generation it has primarily replaced—and consumers, through lower electric prices.
Thus, another key policy question is whether to subsidize existing nuclear plants that are unprofitable. Although economists generally disapprove of operating subsidies because they distort markets and reduce the incentive to innovate, subsidizing existing nuclear plants that are unprofitable is likely to be less costly than replacing those plants with renewable generation. The key is designing the most effective subsidies—namely, those that do not overcompensate existing generators and include incentives to operate efficiently.
The organization of this report is as follows:
- Section I provides a brief history of the nuclear power industry in the U.S.
- Section II examines the industry’s economic decline over the last decade, focusing on the impacts of market distortions, including subsidies for renewable generation.
- Section III looks at today’s economics. Faced with lower natural gas prices, subsidized renewables, and political and environmental opposition, nearly a dozen plants are set to close or are threatened with closure by 2025 while others are scrambling for operating subsidies.
- Section IV considers nuclear power’s future, including whether existing barriers to development can be overcome and what policy and structural changes may be needed to reshape the nation’s electric generating system. Nuclear power’s contribution to the system’s resilience is examined, as are prospects for reducing plant costs.
- Section V offers conclusions and policy recommendations.
I. A Short History of the U.S. Nuclear Power Industry
The first commercial nuclear power plant began generating electricity in December 1957 in Shippingport, Pennsylvania.[16] (See sidebar, Types of Nuclear Power Plants) Originally intended for a nuclear-powered aircraft carrier, whose construction was vetoed by President Eisenhower, the plant’s 60-MW reactor was instead incorporated into a commercial site, constructed in 32 months at a cost of $72.5 million.
|
Types of Nuclear Power Plants |
|
Pressurized Water Reactor (PWR): The most common type of nuclear reactor today. The design originated for submarines. High-pressure water flows through the reactor core, cooling it and acting as a moderator. A separate, lower-pressure water circuit produces the steam that drives the generators.
|
By the early 1960s, the growing demand for electricity and forecasts for continued rapid growth encouraged electric utilities to plan for and begin construction of numerous nuclear plants. The fundamental problem with these plans, however, was that the plants all were effectively one-off projects: there was no standardization of design and construction. That approach was a recipe for disastrous cost overruns that led to fundamental changes in energy policy and the structure of the electric industry.
Electricity demand continued to grow rapidly in the early 1970s, until the 1973 OPEC embargo. The initial impacts of the embargo were limited. But ultimately, the embargo fundamentally changed U.S. energy policy, encapsulated in the 1978 National Energy Act, a series of five major federal laws.
One of these laws, the Public Utilities Regulatory Policies Act (PURPA), ushered in explicit subsidies for wind and solar generation and encouraged development of renewable generation as an alternative to traditional, utility-owned generating resources. Another, the National Energy Conservation Policy Act, changed the views of many state utility regulators about investments in new electric generating capacity.[17]
Consequently, many state regulators turned their focus from rubber-stamp approval of new generating plants to requiring more comprehensive comparisons of the costs of such generation against the costs of various conservation efforts.[18] Then, in 1979, the second oil crisis (spurred by cutbacks in output following the Iranian revolution), along with the accident at Three Mile Island, likely sowed the seeds of the U.S. nuclear industry’s decline.
After TMI, opposition to nuclear power grew because of overwrought fears about the safety of nuclear plants, fears that were inflamed by credulous reporting.[19] It also led to numerous new NRC safety regulations that significantly increased plant construction costs. In addition, TMI raised opposition to the Shoreham nuclear plant in Suffolk County on New York’s Long Island, which was under construction at the time by the Long Island Lighting Company (LILCO).
In 1983, Suffolk County determined that it could not be safely evacuated in the event of a serious accident at the plant. Then-governor Mario Cuomo ordered state officials not to approve any LILCO-sponsored evacuation plan—effectively preventing the plant from operating at full capacity. But the plant was completed in 1984; and in 1985, LILCO received federal permission for low-power (5% power) tests. However, the 1986 accident at Chernobyl[20] caused even more opposition to Shoreham. By 1989, it had become apparent that not enough local communities would sign on to the evacuation plan for the plant ever to open.[21]
On the other side of the continent, the Washington Public Power Supply System (WPPSS) was doing its part to drive a stake through the nuclear industry. WPPSS was started in the 1950s as a means to guarantee electric power to homes and industry in the Northwest. Well-meaning officials believed that building nuclear plants was the best way to supply clean and cheap electricity to customers. Instead, events and human inadequacies produced the largest municipal bond default in U.S. history. The system’s acronym, pronounced “whoops,” came to represent how not to run a public works project.
Planners expected that the demand for electricity in the Northwest would double every 10 years, beyond the capacity of hydropower. WPPSS made plans for a total of five nuclear plants. Two of the plants, proposed in 1971, were to be located at the Hanford Nuclear Reservation, where the U.S. had constructed a uranium enrichment facility during World War II to support the Manhattan Project. Two others—near Satsop, in Grays Harbor County—were proposed the following year. A fifth plant was then planned, again at Hanford.
Several factors combined to ruin construction schedules and to drive costs to three and four times the original estimates. Inflation and design changes constantly plagued all the projects. Builders often got ahead of designers, who modified their drawings to conform to what had been built. Safety changes imposed by NRC increased costs, too, but the biggest cause of delays and overruns was mismanagement of the construction process by WPPSS, whose directors and managers had no experience with nuclear plant construction and who had never undertaken construction of generating plants on this scale. The consequences included poor supervision, shoddy work, and cost overruns caused by work having to be redone.[22]
The spiraling costs, together with reductions in the growth of electricity demand and an emphasis on energy conservation, led to WPPSS canceling two plants and ceasing construction on two others. In 1983, WPPSS declared bankruptcy, resulting in a decade’s worth of litigation to resolve all the competing claims. Ultimately, only Plant 2 was completed.[23]
Electric Industry Restructuring and the Nuclear Industry
In the mid-1990s, efforts began in earnest on the state level to restructure the electric industry. One purpose was to protect ratepayers from the effects of cost overruns and inefficient operations, including nuclear plants. (See sidebar, Nuclear Plant Construction and “Prudent” Utility Decisions.) Under a traditional cost-of-service (COS) regulatory regime, there is little economic incentive for a utility to improve the efficiency of its operations and reduce costs. The reason is that efficiency improvements that reduce operating costs will be reflected in a reduction in a utility’s COS.
|
Nuclear Plant Construction and “Prudent” Utility Decisions |
|
In contrast to the WPPSS plants and those being built by the Tennessee Valley Authority, most nuclear plants were built by investor-owned electric utilities. The same cost overruns led to protracted legal battles that further eroded public support for nuclear power.
|
A second purpose of restructuring was to take advantage of improvements in generation technologies—specifically, high-efficiency gas-fired generators. Some customer groups, particularly large industrial ones, saw an opportunity in restructuring to avoid responsibility for paying the costs of existing, and expensive, generation by purchasing electricity directly from wholesale suppliers.
States pursuing industry restructuring needed to separate their electric utilities’ generation operations, which were generally considered to be competitive, from transmission and distribution functions, which were considered to be natural monopolies. In some cases, states required utilities to spin off generation into separate, unregulated companies. In other cases, states required the utilities to sell their generating assets, including nuclear plants, to the highest bidders.
At the time, many nuclear plants were thought to be unprofitable. Some were operated poorly, resulting in high costs and frequent outages. Others were simply old. Consequently, many nuclear plants were sold off at prices far below their book values (i.e., the remaining undepreciated costs of the plants still carried on utilities’ books).[24] One reason for the low sale prices was expectations that restructuring would lead to lower wholesale electric prices, and hence, lower profitability for these plants.
But after the profit motive was restored to nuclear plant owners, the plants became profitable. Moreover, forecasts of higher natural gas prices led to expectations of greater profitability. Nuclear plant owners, who had been able to purchase plants at low market prices, also found ways to reduce operating costs and improve plant utilization.[25] Some owners began to expand the operating capacity of their plants with what are called “uprates,” as well as file to extend their operating licenses. Nuclear plant ownership also consolidated to exploit economies of scale. Today, for example, Exelon Nuclear owns 22 reactors at 13 sites and is the largest owner of nuclear plants in the U.S.[26]
II. Wholesale Power Markets and the Economic Decline of the Nuclear Industry After 2008
Thanks to huge increases in natural gas production brought about through hydraulic fracturing, natural gas prices collapsed beginning in mid-2008. Lower gas prices, combined with improvements in the efficiency of gas turbines, reduced wholesale electric prices, cutting the profitability of nuclear plants. Meanwhile, the Great Recession that began at the end of 2008 reduced electricity demand, further suppressing wholesale electricity prices. For example, the average price in 2017 was less than half the average price in 2008 at PJM Interconnection, the country’s largest regional transmission organization (RTO), which covers 13 midwestern and mid-Atlantic states. Similar pricing declines have taken place at other RTOs. The trend of generally decreasing average prices (Figure 2) has affected nuclear plant profitability.
 Wind and solar energy have also had a price-suppressive effect on wholesale electric markets as their growth has accelerated owing to subsidies.[27] Basic economics teaches that a supplier will offer goods and services as long as the market price is greater than the marginal cost of production. For example, if the cost of producing one megawatt-hour (MWh) of electricity from a gas-fired generator is $30, the owner of the plant will not offer that electricity into the market at a price below that amount.
Wind and solar energy have also had a price-suppressive effect on wholesale electric markets as their growth has accelerated owing to subsidies.[27] Basic economics teaches that a supplier will offer goods and services as long as the market price is greater than the marginal cost of production. For example, if the cost of producing one megawatt-hour (MWh) of electricity from a gas-fired generator is $30, the owner of the plant will not offer that electricity into the market at a price below that amount.
Because wind and solar photovoltaic both have effectively zero marginal operating costs, they can offer generation into the market at a zero price. In fact, because of the production tax credit (PTC), which now stands at $23/MWh (about $28/MWh on an after-tax basis), wind generators that are eligible for the PTC can offer into the market at below-zero prices and still be profitable. (Negative prices can arise in wholesale electric markets because baseload generators like coal and nuclear plants cannot be shut down and restarted in concert with changes in electricity demand. Nor can they typically adjust their output based on changing demand, called “load following.” Consequently, nuclear and coal plants supply power into the market regardless of market price.) Specifically, wind generators that are eligible for the PTC can generate profitably as long as the market-clearing price is greater than about -$28/MWh.[28]
Although the overall impacts of zero and negative market prices on fossil fuel and nuclear plants have been debated, zero and negative prices have an obvious adverse impact on the profitability of all other generators. When market prices fall below those units’ marginal cost, they must absorb the financial losses.[29]
The effects of increasing percentages of wind and solar generation on wholesale prices have been modeled.[30] Because wind and solar generation are variable, i.e., dependent on whether the sun is shining or the wind is blowing, their output fluctuates over each day. For example, solar generation typically peaks in the afternoon. However, peak demand usually occurs in the early morning and early evening hours. Consequently, market prices during the afternoon tend to fall markedly, but prices for peak demand hours are less affected. The result is what is sometimes called a “duck curve” for wholesale electric prices. The most notable example has taken place in California, where the state produces so much solar power in the afternoons that it must often pay neighboring states to take that power.[31]
In general, as more zero-marginal cost variable resources (VR) like wind and solar are added to the market, the more wholesale prices fall (Figure 3).

Taken to the limit, as wind and solar generation make up larger percentages of the wholesale market, at some point that market will start to collapse. The reason stems from the zero-marginal-cost nature of wind and solar. As more and more of those resources are added, market prices will plummet. Eventually, no generating resources will be able to compete. In fact, if the market were 100% wind and solar, market-clearing prices would be zero and the market would collapse entirely.[32] The wind and solar resources could not themselves remain economically viable without additional out-of-market payments, or a return to some form of cost-based reimbursement similar to reimbursement under traditional COS utility regulation.[33]
This market dilemma, and the need for out-of-market payments to ensure that generating resources can remain economically viable, will need to be addressed if nuclear is to have any long-term future in the U.S.[34]
III. The Economics of the U.S. Nuclear Industry Today
The 98 reactors at 60 commercially operating nuclear plants[35] provided just over 21% of total U.S. electric generation in 2018.[36] That percentage has remained relatively constant since 1990, despite the increase in non-hydroelectric renewable generation and natural gas-fired generation, primarily as a result of the decrease in electricity generated from coal.
The U.S. fleet of nuclear plants is highly efficient. Overall availability (called “capacity factor”) was over 92% in 2018, far higher than any other type of generating resource. Total operating costs for these plants averaged just under $32/MWh—about the same as average fuel costs for coal-fired power plants.[37]
Yet 11 nuclear plants, with capacity totaling over 18,000 MW, are scheduled to close by 2025 or are threatened with closure owing to lower natural gas prices and subsidized renewable generation, an increasing inability to compete in wholesale electricity markets, and political and environmental opposition (Figure 4). The affected plants, which encompass 15 reactors, account for about 18% of the country’s entire nuclear capacity.[38]

In 2018, these plants generated about 124 TWh of electricity every year.[39] By contrast, the combined output of all the nation’s wind generation and utility-scale solar PV plants in 2018 was about 340 TWh.[40]
Another eight plants, with a generating capacity of almost 11,800 MW, currently receive, or are expected to receive, operating subsidies (Figure 5). The rationale for these subsidies has been twofold: (i) to reimburse nuclear plants for their lack of carbon emissions; and (ii) to preserve jobs and local economies.

New York was the first state to provide subsidies for nuclear plants, granting them to Exelon Nuclear’s parent, Exelon Generation, for its James FitzPatrick, R. E. Ginna, and Nine Mile Point plants under the state’s Clean Energy Standard in the form of ZECs (Figure 5).[41] According to an analysis by EnergyWatch, the subsidies now cost New York electric ratepayers just under $500 million per year.[42] The subsidies, which began in April 2017, are scheduled to last until 2029, at an estimated cumulative cost to ratepayers of about $7.6 billion.[43]
In 2016, Illinois’ then-governor, Bruce Rauner, signed the Future Energy Jobs Bill, which provides subsidy payments to Exelon for two plants that the company had threatened to close: Clinton and Quad Cities.[44] The subsidies, whose primary purpose is to retain the 4,200 jobs the plants provide,[45] also take the form of ZECs and are estimated to cost Illinois ratepayers $235 million per year, or about $3.1 billion over their 13-year life span.[46] As one commentator wrote, the way to make money in an era of low electricity prices is to “persuade lawmakers to provide subsidies paid by customers.”[47]
In 2017, Connecticut’s then-governor, Dannel Malloy, signed legislation providing subsidies for zero-carbon energy generators, including the Millstone plant, the only nuclear facility in the state.[48] Dominion Energy, Millstone’s owner, has received initial approval for long-term subsidies.
In 2018, New Jersey governor Phil Murphy signed a bill authorizing ZECs for that state’s nuclear plants at risk of premature retirement,[49] with an estimated cost of $300 million annually.[50] A companion bill requires New Jersey to obtain 50% of the state’s electricity from renewable resources by 2030 and calls for 3,500 MW of offshore wind generation and 2,000 MW of energy storage by 2030.[51] In April 2019, the New Jersey Board of Public Utilities approved subsidies for PSEG’s Hope Creek and Salem nuclear plants, after PSEG had threatened to close them.[52]
Legislation introduced in Ohio in 2017, but still pending, would provide FirstEnergy Solutions, the owner of the Davis-Besse and Perry plants, with “zero-emissions nuclear” (ZEN) subsidies.[53] In 2018, FirstEnergy requested emergency subsidies from the Department of Energy (DOE) to keep its nuclear and coal-fired plants open, in order to provide system “resilience.” (See sidebar, ZECs: Credit or Subsidy?)[54] The Trump administration has yet to act on the request. FirstEnergy has said that if subsidies aren’t granted by either the state or DOE, the Davis-Besse and Perry plants will be closed in 2020 and 2021, respectively.
|
ZECs: Credit or Subsidy? |
|
As discussed previously (Figure 5), subsidies have been granted to a number of nuclear plants. Proponents sometimes claim that zero-emissions credits (ZECs) are not subsidies but payments for a currently unpriced environmental attribute: nuclear energy’s lack of carbon emissions. It is for this reason that the basis for most ZEC values has been the social cost of carbon (SCC).a The SCC, however, is highly controversial, and estimates of its value are fraught with uncertainty.b
|
Similarly, legislation has been introduced in Pennsylvania to subsidize that state’s five nuclear plants. The legislation would add nuclear generation to the state’s Alternative Energy Portfolio Standard.[55] According to the legislation’s sponsor, Rep. Tom Mehaffie, the annual cost of the subsidies to ratepayers would be $500 million.[56] If this legislation is enacted, about 16,000 MW of U.S. nuclear generating capacity would be subsidized for the foreseeable future.
As more nuclear plants that compete in wholesale power markets are granted subsidies, the incentive increases for the remaining plants to obtain them as well, if only to level the playing field. (Nuclear plants owned by vertically integrated electric utilities are compensated based on their overall costs under the traditional COS regulatory framework.) As with all subsidies, such compensation is economically inefficient because it produces market distortions. For example, natural gas-fired generators emit less carbon than coal-fired plants to produce a MWh of electricity. Yet gas generators do not (currently) receive credits for less carbon emissions. Thus, one can argue that coal-fired generators are receiving an anticompetitive subsidy.
As noted earlier, despite the fact that existing nuclear plants are well run and more cost-efficient than ever,[57] economic factors—reduced electricity demand, lower natural gas prices, and, increasingly, subsidies for wind and solar generation—are reducing their profitability, with many plants losing money. Moreover, construction of new nuclear plants has been affected by the same cost overruns and construction delays that have confounded the industry since the 1960s. Other issues, especially the need for permanent disposal of spent nuclear fuel, remain politically intractable.
In the near term, therefore, the nuclear industry does not seem capable of any renaissance. Barring an end to renewable-generation subsidies—both federal tax credits and individual state mandates—and to low natural gas prices made possible by hydraulic fracturing and the resulting increases in gas supplies, wholesale electric prices are unlikely to see significant increases that will bolster the profitability of existing plants that operate in deregulated markets. (Nuclear plants owned by vertically integrated utilities likely will be unaffected.)
Thus, although some nuclear plants will continue to operate profitably, many will not. For example, nuclear scientist Geoffrey Haratyk has assessed the profitability of all 60 U.S. nuclear plants over the 2017–19 period, and estimated that two-thirds of the country’s nuclear capacity would be unprofitable, with average profits ranging between –$29/MWh and +$15/MWh.[58] Curiously, Haratyk’s estimates projected that the Millstone plant in Connecticut, which the state Public Utility Regulatory Authority has determined is eligible for long-term subsidies, would be the most profitable of all 60 plants. He also estimated that plants operating in regulated markets had far worse profitability outlooks. Yet, few, if any, of those plants are likely to be retired because they do not face any competitive pressures to operate more efficiently.
IV. Looking Ahead: Can the Nuclear Industry Survive?
While the U.S. nuclear industry has shrunk, reliance on nuclear power worldwide (along with coal) is increasing, and not just in developing nations. In Australia, for example, which contains significant uranium reserves but has no nuclear plants, Prime Minister Scott Morrison has expressed an interest in developing nuclear power to reduce the costs of electricity.[59] Those costs have doubled in the past decade in that country because of green energy policies emphasizing wind and solar development—current residential prices average over 31 Australian cents per kilowatt-hour (kWh).[60] For its part, the Russian State Atomic Energy Corporation, or Rosatom, is expanding and building plants in a number of countries, including Bangladesh, Egypt, Finland, Hungary, India, and Iran.[61]
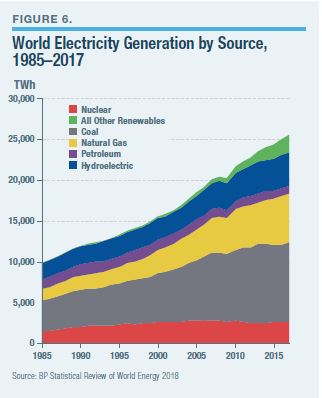 Worldwide, nuclear power accounts for over 10% of all electricity supply (Figure 6).[62] By comparison, all non-hydroelectric renewables accounted for 8.5% of world supply in 2017, even with subsidies.
Worldwide, nuclear power accounts for over 10% of all electricity supply (Figure 6).[62] By comparison, all non-hydroelectric renewables accounted for 8.5% of world supply in 2017, even with subsidies.
Nuclear power provides clear benefits. First, and perhaps most important, it is emissions-free. Whether or not one believes that carbon emissions are problematic, nuclear power emits no air pollutants, such as sulfur dioxide, oxides of nitrogen, and especially particulates, all of which are believed to cause adverse environmental and health impacts.[63]
Second, of all commercial generating resources, nuclear has by far the highest power density, which means that it can generate a lot of power from a small footprint.[64] For example, the Indian Point Energy Center in Westchester County, New York, sits on about 240 acres and provides 2,060 MW of capacity. That’s equivalent to a power density of over 2,100 watts per square meter (w/M2).[65] In contrast, solar and, especially, wind generation have low power densities. Wind generation, for example, even with the largest and most modern turbines, is estimated to have a power density between 0.5 and 1.5 w/M2.[66] Thus, meeting U.S. electricity needs with nuclear power will require much less land than wind and solar power, as many politicians have mandated. Yet, a number of states have established goals to supply electricity solely from renewable energy resources by 2050 or earlier.[67]
Third, electric-grid resilience has been cited by nuclear proponents as one justification for providing subsidies to nuclear plants or, as advocates prefer, paying for another unpriced attribute. (See sidebar, “ZECs: Credit or Subsidy?”) One of these aspects relates to “fuel security”—specifically, the potential for disruptions to fuel supplies relied on by fossil-fuel generating plants. Because nuclear plants are refueled only every 18 months to two years, they are far less vulnerable to supply disruptions than gas-fired generators, which rely on continuous deliveries from natural gas pipelines, and coal plants, which often rely on deliveries via rail.[68] The availability of nuclear generation during “polar vortex” events in the winters of 2014 and 2019, when significant quantities of fossil-fuel generation were often unavailable, demonstrated the ability of nuclear plants to provide system resilience.[69]
Fourth, opponents of nuclear power who advocate for an all-renewable power grid ignore the significant engineering problems associated with maintaining system reliability. Specifically, as more intermittent generation is added to the bulk power grid, it becomes more difficult to ensure that the system operates within critical voltage and frequency limits. If those limits are not maintained, end-use equipment (refrigerators, motors, etc.) can be damaged.[70] In the worst case, a failure to maintain voltage and frequency levels can result in blackouts.
Today, wind and solar facilities are “firmed” by varying the output of natural gas-fired generators to balance changes in wind and solar generation from moment to moment. As the amount of wind and solar generation increases, that becomes more difficult and more costly.[71] Moreover, as a recent report by my Manhattan Institute colleague Mark Mills demonstrates, the holy grail of high-capacity, low-cost battery storage remains a distant dream.[72]
It is possible to provide a rough comparison of the costs to subsidize nuclear plants and the cost of subsidies for wind and solar generation. In 2018, total nuclear generation was just over 807 TWh. If all that generation were paid a subsidy equal to the current New York ZEC price of $17.48/MWh, the annual cost would be $14.1 billion. By contrast, in 2016, the latest year for which data are available, direct federal subsidies for wind and solar generation (tax credits and direct payments) totaled $3.5 billion for 282 TWh of generation, equivalent to $12.41/MWh.[73]
But these direct federal subsidies vastly understate the additional public and private support that wind and solar generators receive to deliver their electricity to customers. Specifically, the federal aid does not include all the indirect subsidies received by wind and solar generators in the form of backup generation, system balancing to ensure that the grid operates within specific voltage and frequency parameters, and the additional costs of building high-voltage transmission lines across the country to deliver wind and utility-scale solar generation to urban demand centers.[74] For example, the 2012 OECD report (cited in n. 71) estimated total bulk power grid costs for onshore wind to be about $20/MWh for a 10% mix of onshore wind in France and Germany, increasing to $24/MWh–$44/MWh for a 20% mix. For solar generation, the OECD report estimated grid-level costs at $36/MWh–$47/MWh with 10% solar generation, increasing to $47/MWh–$83/MWh for a 30% solar generation mix.[75] The higher estimates reflect large investments in new long-distance transmission.
In contrast, the OECD report estimated the total bulk power system costs of nuclear power to be about $2/MWh—notably, with no backup costs whatsoever.[76] Furthermore, because the U.S. is so much larger geographically than individual European countries, the per-MWh costs for transmission system investments would likely be even larger. Additionally, state mandates that require local electric utilities, as well as competitive retail electric suppliers, to obtain increasing quantities of wind and solar generation are themselves an indirect subsidy, which crowds out existing generators.
These comparisons show that the costs to subsidize existing nuclear plants would be far less than the costs of building and operating a bulk power system that relied on wind and solar. And renewable energy advocates who oppose nuclear are not proposing a 30% mix of wind and solar; they are proposing a 100% mix, including using wind, solar, and battery storage to eliminate all fossil-fuel use, not just for electricity generation. The costs and land-use requirements would be immense. (See sidebar, Comparing the Cost of Meeting U.S. Energy Needs with Nuclear vs. Wind/Solar.)
|
Comparing the Cost of Meeting U.S. Energy Needs with Nuclear vs. Wind/Solar |
|
According to EIA, total primary energy consumption (the amount of energy actually consumed in the U.S.) in 2018 was just over 101,000 trillion British thermal units (TBtus), including electric system losses during the course of generation, transmission, and distribution. Ignoring all system losses, total end-use energy consumption was about 76,000 TBtus. Suppose that we could improve conversion efficiency using all-electric sources and reduce the amount of end-use energy consumption to 50,000 TBtus; this would be equivalent to an annual supply of 14,650 TWh of electricity, or about 40 TWh every day, on average.
|
Moreover, nuclear power provides the electric system with what is termed “resilience” against major disruptions. (See sidebar, Power System Reliability vs. Resilience.) For example, in January 2019, a polar vortex led to extremely cold weather in the Midwest and mid-Atlantic. The cold weather caused some coal plants to shut down because of frozen coal piles. Some natural gas generation was disrupted because of insufficient pipeline capacity. Service at only one nuclear plant—Salem, in New Jersey—was disrupted, because of ice.[77]
|
Power System Reliability vs. Resiliencea |
|
One concept that is frequently cited by supporters of nuclear plants is the plants’ ability to provide “resilience” for the bulk power system. (As discussed, the system is the network of generators and high-voltage transmission lines that delivers electricity to local utilities, which distribute that power to customers.)
|
Thus, from the standpoint of the benefits it provides, nuclear power is worth saving. Weighing against these benefits are high costs. Unless it can overcome its history of cost overruns and construction delays, the prospects for a thriving nuclear industry will be bleak.
The other issue most often raised by critics of nuclear power is permanent storage and disposal of spent fuel. For nuclear power to remain a viable energy technology, this issue must be addressed. In fact, 14 states, including many with nuclear plants currently operating or retired, have prohibitions or restrictions on construction of new plants until a permanent repository for high-level waste has been identified.[78] Minnesota, for example, has an outright ban on new plant construction. Ironically, in states with nuclear plants, spent nuclear fuel is stored at the plants, initially in spent-fuel pools and then in dry casks.
Fortunately, as a number of studies have discussed, disposing of spent nuclear fuel is not a technological issue.[79] Rather, it is a political one. Spent fuel, which remains radioactive for thousands of years, can be disposed of safely. Finland has taken the lead on the issue and is constructing a permanent underground depository. The project has been supported by the government and, most important, by the local community.[80] France, which relies on nuclear power for three-fourths of its electricity, has yet to develop a permanent underground depository, owing to opposition to siting such a facility. However, unlike the U.S., France reprocesses spent nuclear fuel,[81] which creates additional usable fuel, and puts the remaining nuclear waste in temporary storage facilities.[82]
In its most recent budget plan, the Trump administration has proposed to restart Yucca Mountain, the site that was designated by Congress in 1987 as a permanent repository in Nevada.[83] However, the efforts to restart work are opposed by Nevada’s two senators and Democratic congressional leaders.[84] Thus, efforts to develop a permanent repository, whether at Yucca Mountain or elsewhere, are sure to be opposed bitterly.
It seems that the only way the U.S. is likely to solve this political issue is to follow Finland’s approach, which was to identify locations that are geologically suited and then discuss a repository with the local populace, who may view it as a booster for their economy. For example, the Waste Isolation Pilot Project (WIPP), which stores mid-level nuclear waste and is located just south of Carlsbad, New Mexico, is strongly supported by the local community because of its economic benefits.[85]
Prospects for Reducing Nuclear Plant Costs
The primary cause of cost overruns in the past has been the lack of standardization in design and construction. Plants built in the 1960s through the 1980s became, in effect, one-off designs owing to changing design requirements. More recently, efforts to build new reactors, such as the two units being added to the Southern Company’s Vogtle plant and the SCANA Corporation’s now-abandoned Santee Cooper facility, have been hampered by a lack of manufacturing and construction expertise.[86] The knowledge gained from building plants decades ago effectively was “lost” over time. Thus, in addition to design standardization, manufacturing and construction expertise must be regained.
The major effort toward standardization is the development of small modular reactors (SMRs). Currently, the most advanced SMR design is one developed by NuScale. The NuScale reactor is now undergoing design certification review by the Nuclear Regulatory Commission.[87] That certification is expected to be completed in August 2020. The NuScale SMR houses a reactor, steam generator, and pressurizer in a single container, which is 76 feet long and 15 feet wide and weighs 700 tons.[88] The pressurized water reactor (PWR) design has fully passive safety systems, precluding the need for active intervention to shut the reactor down. This means, the designers say, that there can be no core meltdowns, such as those that took place at the TMI plant and at Fukushima Daiichi.[89] The idea is to manufacture these units and transport them to the sites where they will be installed.[90]
The first NuScale SMRs are slated to be installed at the Idaho National Laboratory in Idaho Falls and to be operational by 2026.[91] The plant will be owned by the Utah Associated Municipal Power Systems and operated by Energy Northwest, which runs the Columbia Nuclear Generating Station near Richland, Washington (the former WPPSS 2 plant). The new plant will consist of 12 60-MW NuScale SMRs. The current projected cost of the plant is about $3 billion, or about $4,200/kW.[92]
At this time, SMRs appear to be the best hope for a nuclear renaissance.[93] But given the past history of nuclear power, one would be forgiven for doubting that the Idaho plant’s cost will come in anywhere close to the $3 billion estimate. A higher actual cost will not be surprising because, although the NuScale plant is supposed to reduce costs owing to its modular design, the plant will still be the first one built, and first-mover manufacturing costs are almost always higher than forecast because of unanticipated complexities.
If SMR technology can deliver on its promise of lower costs, the prospects for the economic viability of nuclear power will improve. Even so, private-sector investment in nuclear plants entails huge financial risk. The current structure of wholesale power markets in the U.S. discourages such “bet-the-company” investments. (Consider what happened to SCANA: one reason that the company was recently purchased by Dominion Energy was that cost overruns at SCANA’s ill-fated Santee Cooper project and the diminishing prospects for recovering those costs from ratepayers had cratered its stock price.) If the nuclear industry is to survive, it will likely continue to require subsidies, at least for the next decade or so.
A comprehensive MIT study proposes a half-dozen ways to address concerns about cost overruns. The recommendations are: (1) using proven construction management practices to increase the likelihood of success, including the use of manufacturers with a solid supply chain and skilled workers; (2) employing modular construction techniques; (3) employing passive safety designs; (4) creating a level playing field to allow all low-carbon technologies, including nuclear, to compete on their own merits; (5) identifying government-approved sites where companies can build test reactors; and (6) initiating government-funded programs to share regulatory licensing costs, along with research and development costs, and also to share production credits to reward successful demonstrations of new designs.[94]
The first three recommendations recognize that, as discussed previously, the primary causes of nuclear plant cost overruns stem from complex one-off designs, built on-site, by companies that lack the expertise and experience to construct such plants. Providing sites where test reactors can be built and evaluated is also important, much as building prototypes of products can identify design and manufacturing problems at an early stage, rather than in the middle of constructing a commercial facility.
A level playing field for all low-carbon technologies, rather than the current hodgepodge of state and federal policies and renewable energy tax credits, would improve the ability of nuclear power to be cost-competitive. However, it would not solve the fundamental problems facing wholesale electric markets created by growing quantities of renewable resources with zero marginal cost. Moreover, as discussed below, despite various claims that broad-based carbon taxes would either not harm or even benefit the U.S. economy, such taxes likely would have significant adverse impacts on the economy, would not “solve” the climate change issue at all, and would disproportionately harm lower-income Americans and those living in rural areas.
As for government subsidies and tax credits, such policy instruments that are designed to be temporary are extremely difficult to end. The production tax credit (PTC), for example, was initially designed to assist renewable energy development (primarily wind generators), improve technology, and reduce costs. Today, more than a quarter-century later, there is no economic rationale for continuing such credits. PTC has been slated to expire before, only to be resurrected by Congress.[95]
Evaluating Policy Alternatives to Preserve Existing Nuclear Power
Policies to address nuclear power can be separated into those designed to preserve existing nuclear plants and those designed to promote development and construction of new plants. Geoffrey Haratyk, for example, proposed a number of policies to address nuclear plants that operate in deregulated electric markets (Figure 7).
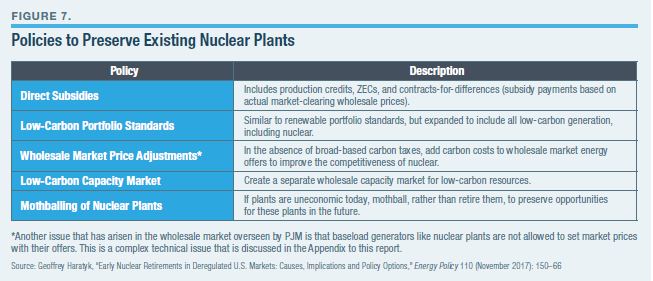
The primary policy instrument being used to preserve existing nuclear plants is the ZEC. From an economic standpoint, ZECs are inefficient because they are based, at least to some extent, on estimates of the social cost of carbon (SCC). Those estimates are fraught with uncertainty and based on models that some, such as MIT economics professor Robert Pindyk, have characterized as virtually useless for policymaking.[96]
For example, ZECs received by Exelon’s nuclear plants in Illinois are currently set at $16.50/MWh, subject to adjustments based on a market price index.[97]
The price will increase by $1/MWh annually, beginning in 2023. In New York, the initial ZEC value was based on an SCC value of $42/ton and initially set at $17.48/MWh. The ZEC value will change over time to reflect shifts in SCC values, inflation, and wholesale electric prices in New York.[98] In 2018, the average wholesale price in New York was $44.92/MWh, a 23% increase over 2017’s average price of $36.56/MWh.[99] Thus, in 2017, ZECs were equal to roughly half the wholesale price of electricity; in 2018, they were almost 40% of the price. This subsidy is lower than the wind PTC, which is $28/MWh on a pretax basis, almost two-thirds of the average wholesale price in 2018. And, as discussed previously, wind and solar generation receive indirect subsidies for grid-related costs, especially backup generation.
One advantage of ZECs is that they are controlled by regulators and policymakers, who can thus target them solely to those plants in need of subsidization. The disadvantage of ZECs is that they are controlled by regulators and policymakers. Typically, regulators are not bound by past regulators’ decisions. Moreover, political pressure, rather than economic need, can affect which plants receive subsidies and the level of those subsidies. For example, Haratyk (2017) forecast that the three New York nuclear plants currently receiving ZECs—FitzPatrick, Ginna, and Nine Mile Point—ranked among the 10 most profitable plants in the nation. Whether Haratyk’s estimates are accurate is unknown because reliable data on the plants’ profitability are not publicly available.
Another problem with direct subsidies such as ZECs is that they are difficult to set correctly and thus further distort wholesale electric markets, which are already distorted because of subsidies for wind and solar generation. Using subsidies to counteract the distortions caused by other subsidies is a prescription for a failed wholesale market. Tying ZEC values to arbitrary SCC values is problematic from the standpoint of economic efficiency, although it is convenient.[100]
A more straightforward approach for subsidizing existing nuclear plants would be to use what are called “contracts-for-differences” (CfD). A CfD would adjust the subsidy payment based on the actual market-clearing wholesale price. Thus, if a nuclear plant’s marginal cost is $40/MWh and the wholesale price of electricity is $30/MWh, the plant would be paid the difference: $10/MWh. If, however, the wholesale price were greater than $40/MWh, the plant might be allowed to keep the difference or, depending on the type of CfD, be required to refund the difference.[101]
A CfD approach could also be combined with a performance-improvement requirement, such that nuclear plants receiving such subsidies would have an economic incentive to improve performance, similar to electric utilities that operate under performance-based regulation regimes.[102]
A third approach would be to compensate at-risk nuclear plants on a COS basis, much as generating plants owned by vertically integrated utilities are compensated. For example, RTOs allow plants that are uneconomic, but are needed to ensure reliability, to operate under cost-based, “reliability must-run” (RMR) agreements. However, such contracts can be controversial and have their own issues, such as determining an appropriate return on capital investment for the plant. Moreover, a COS framework, unlike a competitive market, provides no incentive to improve operating efficiency.
Haratyk (2017) proposed two other mechanisms: adjusting supplier offer prices based on their carbon emissions; and creating a separate, low-carbon capacity market.
There are several problems with the former. First, as discussed, it requires establishing a price on carbon, which may be arbitrary and have little to do with the actual external costs of carbon emissions. Second, adding a carbon price to supplier offers does nothing to address the market distortions created by subsidized wind and solar plants. Third, it will lead to higher electric prices that harm consumers, especially if the additional electricity costs paid by consumers exceeds the amount of the subsidy required by plants to be made whole.
As for a low-carbon capacity mechanism, its implementation would be fraught with complexities and subject to debate. Since they were first introduced in the mid-2000s, electric capacity markets have been controversial and frequently changed. Adding yet another layer of complexity to these markets is unlikely to enhance their function. Arbitrarily limiting a capacity market to “low-carbon” resources—especially when wind and solar generation are inherently intermittent—is unlikely to succeed. And, as Haratyk notes, if such a mechanism accelerated retirements of fossil-fuel resources, especially peaking units, system reliability could be compromised, which likely would require more out-of-market RMR contracts.
Finally, policymakers could impose broad-based carbon taxes or carbon cap-and-trade systems. Although such mechanisms would avoid the additional distortions to wholesale electric markets caused by ZECs, unilaterally imposing a carbon tax in the U.S. would raise prices on almost all goods and services and reduce economic growth. Even a “revenue-neutral” carbon tax would likely have adverse consequences, especially on lower-income consumers and those living and working in rural areas.[103] Moreover, a unilaterally imposed carbon tax would have no measurable impact on world climate.[104] And there is no assurance that a given carbon tax would “save” existing nuclear plants.
Evaluating Policy Alternatives to Encourage New Nuclear Plants
New nuclear plant development and construction in the U.S. likely will occur only with government assistance and changes in regulatory frameworks suggested in Figure 8. Government assistance can take the form of production and investment tax credits for nuclear plants, similar to those for renewable generation. It can also take the form of loan guarantees.

However, direct government assistance will do nothing to reduce cost overruns. In fact, it can reduce the incentive to avoid them. As is well known to economists, providing direct subsidies reduces the incentive to lower costs and improve competitiveness, including through technological innovation.
It is doubtful that any new large nuclear plants will be built without government loan guarantees, even for plants proposed by vertically integrated and regulated electric utilities.[105] The financial risks simply are too great for private investors.
The “bet-the-company” risks of large nuclear plants thus favor development of SMRs. If SMR costs can be controlled effectively and if manufacturing and construction expertise to build these plants can be developed, then SMRs are likely to be the most promising nuclear path. SMR technologies therefore should be encouraged and supported.
Finally, it may be possible to develop new regulatory frameworks for building and operating nuclear plants that combine cost guarantees with performance incentives. Some electric utilities already operate under performance-based regulatory regimes (PBR), which allow those utilities to capture a portion of cost savings for their shareholders.
A similar approach could be applied to nuclear plant construction and operation. For example, a combination of loan guarantees and backstop cost guarantees would allow the government to reduce, but not eliminate, financial risks to investors. This could then be coupled with a regulatory regime that provided an economic incentive for reduced costs and improved operations.
Nuclear Power and Electrification Policies
Several states, notably New York and California, have proposed to eliminate fossil-fuel use by electrifying their economies. This would entail replacing internal combustion vehicles with electric vehicles, swapping out oil for natural gas furnaces, and so forth. The “Green New Deal” proposes to do the same for the entire country.
Regardless of the merits or economic reality of these proposals, such mandates will greatly increase the demand for electricity. In New York, for example, electricity accounts for only about one-seventh of total end-use energy consumption.[106]
Meeting this increased demand for electricity by relying solely on wind and solar resources with low power densities is unrealistic. The land requirements would be staggering. It would require huge investments in high-voltage transmission lines that crisscross the country delivering electricity to urban load centers. And, as my Manhattan Institute colleague Robert Bryce has noted, opposition to siting large-scale renewable energy facilities continues to grow.[107] What’s more, because wind and solar are intermittent, huge investments in battery storage will be required, costing billions, if not trillions, of dollars.[108] Regardless of the merits of electrification policies, absent fundamental technological leaps, meeting these renewable-energy goals will be impossible without nuclear power.
V. Conclusions and Policy Recommendations
Nuclear power provides valuable benefits. It is highly reliable, emissions-free, and offers far greater power densities than renewable resources. It has proved its value in extreme weather events, when fossil-fuel generation has been unable to deliver because of supply constraints and operational issues. It also provides additional diversity, which can reduce the adverse impacts of fuel price shocks. And, unlike intermittent wind and solar, nuclear power does not require backup generation or storage. Large-scale implementation of wind and solar generation to meet emissions reduction goals, especially if those goals include substituting electricity for fossil-fuel consumption, is simply not feasible, given the land requirements and the cost of battery storage needed to provide reliable supplies.[109]
Against that background, some nuclear plants cannot compete in wholesale electric markets, even though the industry as a whole has reduced costs and significantly improved operating efficiency. Low natural gas prices and highly efficient gas-fired generators have reduced market prices. So have subsidies for solar and, especially, wind generation, which, because of the federal PTC, can operate profitably even when electricity prices fall below zero.
As noted in Figure 5, eight nuclear plants are or soon will be receiving subsidies. Other nuclear plant owners are clamoring for subsidies of their own, based on claims of an inability to compete as well as political appeals to save jobs and preserve local economies. These subsidies are inefficient and distort wholesale power markets. They likely will have adverse long-term consequences because subsidies distort market signals and affect supplier decisions to enter and exit markets. Nevertheless, the cost to directly subsidize all existing nuclear plants using the current subsidy being paid in New York would be far less than the costs of direct and, especially, indirect subsidies for wind and solar generation.
The most efficient way to assist the nuclear industry would be to impose a nationwide carbon tax. But doing so would have adverse impacts on the U.S. economy, harm consumers—especially lower-income and rural consumers—and, if imposed unilaterally, have no impact on world climate. Thus, subsidizing some uncompetitive nuclear plants is likely the least adverse solution to preserving emissions-free generation, maintaining expertise in nuclear plant operations, and ensuring a reliable and resilient power system.
As electricity becomes ever more important to the U.S. economy, especially with some politicians demanding electrification to combat climate change, nuclear takes on even more significance because it is both clean and reliable. Wind and solar generation will not be able to meet increased demand arising from electrification. The land and storage requirements are unrealistic. Also, the costs of expanding the high-voltage transmission system grid and, especially, the costs of battery storage are prohibitive.
At this time, the best hope for the nuclear industry appears to be SMR technology. If this technology can be developed successfully and the cost savings from modular design and construction realized, the industry could experience a renaissance, while reducing carbon emissions significantly.
Recommendations
- Eliminate renewable generation subsidies at the state and federal level, including federal tax credits, state renewable portfolio standards, and feed-in tariffs for renewable resources. Such subsidies continue to distort wholesale power markets. Because wind and solar proponents have proclaimed these resources are already, or will be, cost-competitive with fossil-fuel generation,[110] all such subsidies should be allowed to expire.
- For owners of existing nuclear plants who are requesting subsidies in order to remain competitive, two recommendations: first, tie those subsidies to wholesale market prices of electricity using contracts-for-differences; and second, combine them with performance incentives that require the owners to improve the operating efficiency of their plants over time. Moreover, before subsidies are granted for a nuclear plant, a comprehensive cost-benefit analysis should be performed to determine whether the magnitude of the subsidies needed to prevent closure makes sense, or instead is so large that building replacement generating capacity is a lower-cost alternative.
- Policymakers should resist subsidizing existing nuclear plants solely to “save” jobs and local economies. Such efforts, like most government economic development programs, merely transfer wealth from large groups of consumers and taxpayers to other groups.
- To develop new nuclear capacity, provide government loan guarantees, along with performance incentives that require investors to bear a portion of the financial risk.
- Require the developers of new nuclear technologies who receive government money to prove that their reactors are safer and more reliable than existing reactors. Furthermore, require them to meet well-defined cost and deployment goals.
- Develop public-private partnerships that will leverage existing nuclear-focused DOE facilities like Idaho National Laboratory and Oak Ridge National Laboratory. Those labs can be used to test and evaluate new nuclear technologies. Test reactor sites can also be used to explore new manufacturing techniques.
- Address the current political logjam over a permanent spent-fuel repository by identifying communities near geologically suitable sites that wish to host such a depository with the promise of local jobs and improved economic growth.
Appendix: Price Formation in the PJM Wholesale Electric Energy Market
PJM Interconnection is the nation’s largest regional transmission organization (RTO), covering 13 midwestern and mid-Atlantic states. To appreciate the current problem with prices in PJM’s wholesale electric market, and with PJM’s not allowing baseload generation to set those prices, it helps to understand why electric markets are different from, say, the market for wheat.
In most markets, individual suppliers make their own decisions about what to produce and when. For example, Farmer Jones can decide how many acres of wheat to plant this year without first consulting Farmer Smith. Similarly, Farmer Smith can decide to overhaul his tractor today without first consulting Farmer Jones. They make all their decisions independently. The same is true for large manufacturers. Apple does not need to coordinate with Dell before deciding how many computers it will manufacture. In fact, in many markets, coordinating with one’s rivals can be unlawful.
Another characteristic of many competitive markets is that, as more goods and services are produced, the cost of each additional unit—whether a bushel of corn or a kWh of electricity—either stays constant or increases. For example, Farmer Jones will plant his most productive land first because the cost of each bushel of corn will be lowest. As he increases the amount of corn he plants, he will use less productive land, resulting in additional bushels of corn produced at an increasing cost. That increasing cost is the variable or “marginal” cost. Moreover, Farmer Jones can decide to produce just a little more or a lot, depending on market prices. Thus, he can decide to plant just one more acre, 1,000 more acres, or anything in between, depending on how much land he owns.
 The collective decisions of individual farmers result in a market supply curve “S” like that in Figure A-1. This is the type of supply curve shown in introductory economics textbooks, one that looks like a smooth line or curve.
The collective decisions of individual farmers result in a market supply curve “S” like that in Figure A-1. This is the type of supply curve shown in introductory economics textbooks, one that looks like a smooth line or curve.
Figure A-1 also shows the market demand curve “D.” The market demand curve slopes downward because consumption increases as the price falls. The competitive, or market-clearing, price, P*, is where the supply curve (“S”) crosses the demand curve (Point A). At this price, a total of Q* is sold. As demand increases, the market price increases. This process of marginal costs setting the market price is called “price formation.” Again, the two key factors that underlie this textbook competitive market are: (i) individual decisions made by suppliers; and (ii) small increments of production.
Electricity markets are far more complex than this textbook example, for two primary reasons. First, electricity production is “lumpy.” While the output from some generating plants can be ramped up and down, allowing them to generate more or less electricity, other plants’ outputs, including the output of nuclear plants, are fixed. In effect, these latter plants operate either “on” or “off,” much like a light switch. This is true of most always-on baseload power plants, which are designed to run at full capacity all the time. The amount of electricity they generate cannot be adjusted up and down. (An analogy is a car that has two speeds: zero and 60 miles per hour.) This “on” or “off” nature for baseload generators is why they are sometimes called “inflexible” generators.
The second reason is that plant owners cannot decide how much electricity to produce independently. Instead, PJM’s system operators coordinate the output of more than 1,000 generating plants at all times to ensure that the amount of electricity produced exactly matches electricity demand and at the lowest cost.
To do this, PJM must account for many complicating factors that never appear in a textbook supply-and-demand chart. These factors include: (i) the costs to start up and shut down individual generating units; and (ii) the locations of the plants and whether there is sufficient high-voltage transmission capacity to deliver electricity to where it is needed, such as a faraway city. The technical term for this is “security-constrained economic dispatch.” In practice, it requires solving a difficult math problem.
Rather than simply ordering specific plants to operate or shut down each day, PJM relies on its competitive market to determine which generators will run. Specifically, each day, PJM collects offers from most generators to supply electricity at various prices into the market for the following day. PJM then compares these offers with its day-in-advance (day-ahead) forecast of electricity demand and determines which generators will operate, subject to any other constraints, such as transmission capacity.
 However, the inflexible nature of most baseload generators makes PJM’s “least-cost” scheduling problem more complex. A simple numerical example can explain why. Consider an electricity market with two generators: the first must always operate at a fixed output level of 100 MW and costs $20/MWh to run; the second can flexibly produce between 1 MW and 100 MW of output at a marginal cost of $10/MWh plus $0.10/MWh for each incremental MW. In other words, if the flexible unit produces 50 MW, the marginal cost of the 50th MW is $15/MWh ($10 + 50 x $0.10). Figure A-2 summarizes these values.
However, the inflexible nature of most baseload generators makes PJM’s “least-cost” scheduling problem more complex. A simple numerical example can explain why. Consider an electricity market with two generators: the first must always operate at a fixed output level of 100 MW and costs $20/MWh to run; the second can flexibly produce between 1 MW and 100 MW of output at a marginal cost of $10/MWh plus $0.10/MWh for each incremental MW. In other words, if the flexible unit produces 50 MW, the marginal cost of the 50th MW is $15/MWh ($10 + 50 x $0.10). Figure A-2 summarizes these values.
If electricity demand is less than or equal to 100 MW during a given hour, Generator 2 should be selected because it provides electricity at a lower cost than Generator 1. For example, if the load is 50 MW, Generator 2 can meet the entire demand, and its marginal cost will be $15/MWh.
But suppose that demand increases to 120 MW. Since Generator 2 can supply only 100 MW, PJM needs Generator 1’s output. But because Generator 1 is inflexible and must produce its full 100 MW, PJM tells Generator 2 to reduce its output to just 20 MW.
Generator 1 is the marginal generator because its marginal cost, $20/MWh, is always greater than the marginal cost of Generator 2. Hence, in a typical competitive market, the market price would be $20/MWh. However, because current PJM rules do not allow Generator 1’s marginal cost of $20/MWh to set the market price, the actual market price is based on the marginal cost of Generator 2, which, when it is producing 20 MW, is $12/MWh.
Because of this inconsistency, instead of having the steady upward slope of the curve in Figure A-1, the marginal cost (MC) curve increases to $20/MWh, then decreases back down to $10/MWh, and starts increasing again as the flexible unit is called on to produce more output to meet demand (Figure A-3).
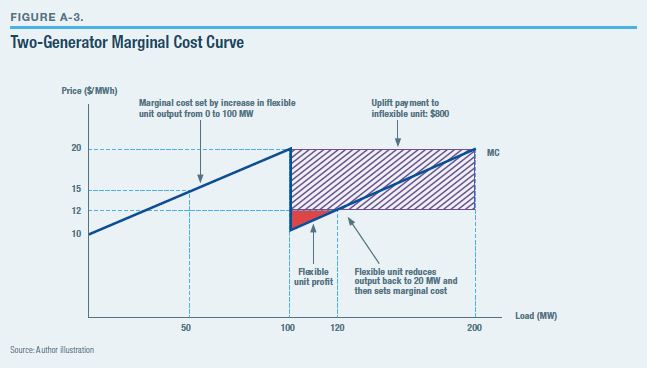
These scissor-shaped MC curves create several problems in the PJM market because marginal cost determines the market price that all generators are paid. Generator 2 can operate profitably—it produces 20 MW and is paid $12/MWh, resulting in total profits of $20 (the small red triangle in Figure A-3).[111] But because Generator 1’s marginal cost is $20/MWh, it loses $8/MWh, or $800 each hour (the purple rectangle in A-3).
PJM cannot force generators to operate at a loss. Therefore, it must compensate Generator 1 for the $800 loss. This out-of-market compensation, called “uplift,” is ultimately paid by electricity consumers. But what is especially perverse is that, under PJM’s current pricing rules, inflexible units can be penalized financially for being available, even when they provide needed resilience.
The reason is that most of these units have lead times of greater than 24 hours. (In other words, it takes more than 24 hours to start them up and have them available for the grid operator to dispatch.) Thus, they cannot offer electricity into the day-ahead market and are not eligible for uplift payments. Instead, inflexible generating units must simply offer power into the market, accepting whatever is the resulting market-clearing price. When that price is zero, or even negative, inflexible units hemorrhage money.
Although this pricing problem has always been an issue with PJM, it has been exacerbated in recent years, especially at night and on weekends, when electricity demand is lowest, as more flexible generation has been added, such as gas-fired generators and, especially, wind turbines. (As noted earlier, because of the federal PTC, wind generators can operate profitably even if market prices are zero or negative.)
Solving the Price Formation Problem
So why not simply replace all of PJM’s inflexible generating units with flexible ones? There are two reasons: cost and resilience. As discussed above, many inflexible units are less costly to operate than flexible ones, and they provide additional value for consumers because they are always on.
Inflexible units are key contributors to ensuring a resilient and reliable electric system, such as providing power during a cold snap. Not only would premature retirement of these units affect PJM’s ability to meet peak demand; it would also reduce the diversity of generating resources. If all coal and nuclear generation were shut down and replaced with gas-fired generation, a disruption in natural gas supplies or a spike in gas prices would have a severe impact on consumers.
PJM has proposed changing its wholesale market pricing rule to mirror that of several other RTOs, including the Midcontinent Independent System Operator and ISO New England. The PJM rule change, which must be agreed to by PJM participants and approved by the Federal Energy Regulatory Commission, would allow the marginal costs of inflexible units to set market prices, which would eliminate the scissor-shaped marginal-cost problem. The rule change would also equitably compensate inflexible units for the value they provide by always being available.
Suppose that demand is again 120 MW. PJM needs the output of the inflexible unit, which is 100 MW, to meet demand. Thus, the flexible unit’s output again is reduced to 20 MW. Now, however, the market-clearing price is $20/MWh, eliminating the uplift payment (Figure A-4). At this price, the flexible unit would choose to operate at its maximum 100-MW capacity, and its total profit would be $500.[112] But because PJM requires it to reduce its output, the unit’s actual profit is $20. Thus, PJM pays the flexible unit an additional $480 in market compensation—the same amount the unit would earn in a fully competitive market.

Although the market price in this simple example increases from $12/MWh to $20/MWh, the more accurate price signal means that consumers will save in the long run because plant investment and retirement decisions will be more efficient.
Endnotes
Acknowledgments
Connor Harris, a policy analyst at the Manhattan Institute, provided research assistance for this report.
Are you interested in supporting the Manhattan Institute’s public-interest research and journalism? As a 501(c)(3) nonprofit, donations in support of MI and its scholars’ work are fully tax-deductible as provided by law (EIN #13-2912529).